こんにちわ、訪問ありがとうございます!
はじめに
以前の記事「小学校算数3年生の単元と項目」で内容一覧を、具体的には『 内容領域ごとの「単元名」「項目名」』をご紹介しました。

それだけでも十分かもしれませんが、学習指導要領 公式解説には、なるほど!と思う詳しい内容が沢山載っています。
家庭学習をサポートする上で、知っていて損はないと思います。よって、公式解説を基にまとめた「項目の詳細説明」を、上記でご紹介した「項目名」に沿って 一覧にして ご紹介しています。
一度にご紹介するとボリュームが多くなりすぎますので、領域ごとに記事を分けています。さらに、内部もボリューミーな領域は、1~3単元ずつに分けています!(特に【数と計算】は多いです(-o-;))
それでは今回は【数と計算】5回目、「小学校算数3年生の項目詳細【数と計算】⑤」です、見ていきましょう!

【数と計算】領域について

3年生の単元一覧
3年生で学習する【数と計算】領域の単元は、以下になります;
【数と計算】 – 単元一覧 :3年生
※ 左の番号は当ブログでの領域内の記事番号です、算数的な意味等はありません。m(_ _)m
各単元の項目詳細
以下より、算数3年生の【数と計算】領域中の単元「分数について」「分数の加法・減法」の各項目について、詳細を どんどん ご紹介していきます!
- 各単元ごとに「項目名」「項目詳細」が記載してあります
分数について
- 分数の「分母」「分子」という用語 および 表し方のルールを知り、分数を正しく表せるようにする
- 具体的な物を「等分してできる部分」の大きさを表すのに、分数が用いられることを知る
(例:ピザ 3/5 枚)
- 測定などで「端数部分の大きさ」を表すのに、分数でも表せることを知る
(例:水 3/5 L)
- まず、「数の基本の単位」が「1」であることを 改めて認識する
(→ 数量や順序、などと言った「数の使われ方」ではなく、他意のない「数そのもの」で、つまり 『「数」という概念』 において、「基本となる数」が「1」です)
(例:「1」が幾つ集まった数なのか、が、1,2,3,4…) - 同様に、同じ分母を持つ分数達にとって、「1/その分母 」という、「分子が1」の状態の分数を、『「その分母である分数」の基本となる数』 という考え方で用いる見方があることを知る
(例:「1/5」が幾つ集まった数か、が、1/5、2/5、3/5、4/5 …) - 「1/その分母 」という分数を、「その分母を持つ分数」の「数としての基本の単位 」としても見れるようにする
(※ 分数がこの考え方で用いられる際、分子が1のその分数は「単位分数」と呼ばれます )
- 「分子が1である分数」が その分母の分数の「単位分数」であり、分子の大きさが1ではない分数も「単位分数が幾つ分か」という考え方でも表せることを知る
(例: 2/3 は 1/3 が2つ集まった数、や、3/4 は 1/4 が3つ集まった数)
(→ 1より大きい分数になっても 考え方は同じで、5/4 は 1/4 が5つ集まった数) - 単位分数は、1/3・1/4・1/5 など、数の大きさの単位として 都合のよい大きさ(その状況に都合の良い分母)を選ぶことができる
(→ 整数では 10 や 100 など、小数では、0.1(1/10)や 0.01(1/100)など、「大きさの単位となれる数」に縛りがある) - このような点から、分数で表す利便性を感じる
- 単位分数の大きさに着目して、分数でも数を比べられることを理解する
(例:2/5 は 1/5 が2つ分、4/5 は 1/5 が 4つ分、と捉えると、どちらが大きいか比べられる)
- 上記までの使われ方を通して、分数の意味について、以下の捉え方ができるようになる;
- ① 実際の物を3等分したものの、二つ分の大きさである
- ② 2/3L、2/3mのように、測定したときの量の大きさも表せる
- ③ 1を3等分したもの(単位分数である1/3)の、二つ分の大きさである(つまり1/3 が2つ集まっている)
- ④ AはBの2/3というように Bを1としたときのAの大きさの割合を表す
- ⑤ 整数の除法「2÷3」の結果(商)を表す
※ 分数が上記①~⑤の意味で用いられている際、「そのように捉えられ用いられている分数」にそれぞれ名前があります;
(ややこしいですが、分数自体の種類分け ではありません)
①分割分数、②量分数、③単位分数、④割合分数、⑤商分数
と呼ばれます。(③については 単位分数なのは 集まった後の 2/3 ではなく 一つ分である 1/3 の方。)1つの分数に複数の捉え方を同時に用いる場合も珍しくありません。この5つは、算数指導のために便宜上分けた、といったところもあるみたいです。
※ この①~⑤についてもう少し詳しく、この単元の最後に「★分数の補足」としてまとめています!「そもそも分数って何」も合わせて記載していますので、よければご一読ください!
⇒ 「★分数の補足」へ!
- 簡単な分数(1/10など)の数直線上の位置を理解して、分数を「数」として捉えることができるようにする
- 同分母どうしの場合は、単位分数の個数に着目することによって、分子の大きさを比べることで、分数の大きさを比べることができることに気付くようにする
- 1という整数を、数直線上に表す過程で、必要に応じて10/10 とも見れるようにする
- 小数の 0.1 と分数の 1/10 などを、数直線の上下に同時に表すなどで、同じ大きさの「数」であることを実感できるようにする
- 小数と同時に数直線上に表すことにより、分数も「数」であることの理解を深める
- 数の概念としての1には、表記として「1」以外にも、小数部分も表して 1.0 や、分数では 10/10 や 2/2、3/3 などがあること、を理解できるようにし、必要に応じた表記で使えるようにする
★ 分数の補足

分数の捉え方や用いられ方、について考え出す前に、最初に「分数って何?」を考えたいと思います。
- 分数とは、 数の表し方の一つで、「数1/数2」という形で表します
- 値は「数1」を「数2」で割った数です
- 「数1」を分子、「数2」を分母と言います
先の①~⑤のように、分数は場合により様々な捉え方や用いられ方がありますが、それは「分数というもの」がどういう見方使われ方をされるか、であり、ではその『「分数というもの」とは一体何?』 に着目した時、シンプルにこの三文です。数1、数2は、分母が0はダメ、以外は、かなり自由です(複素数ではない数になってくると分かりません、スミマセン)。
もっとシンプルに縮めると、分数は「数の表し方の一つ」です。ややこしいところですが、「数の種類の一つではない」のです。
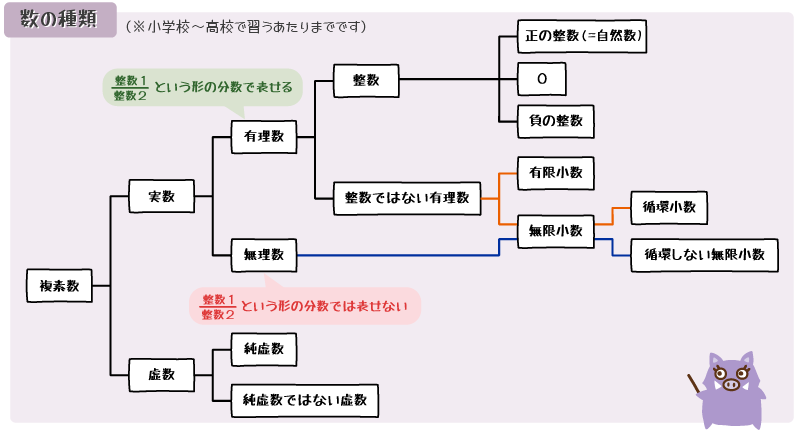
ここを少し掘り下げますと、「数の種類ではない」ので、数の種類分けでは、整数か分数か、という判断基準では分けません(ざっくり掴むための図などでは整数 or 分数と書いてあることもあるかもしれません)。「数の種類」のカテゴリとして挙がってくるのは、整数(正・0・負)、有理数・無理数、実数・虚数、などです。(複素数を超える範囲の数は 作成者では もはや分からず スミマセンmm)
でも「数の表し方」である分数が、このような「数の種類分け」に無関係なワケでもありません。むしろガッツリ関わっており、「整数だけを用いて 分数という表し方が 可能な数か 否か」は、「有理数・無理数」の境界線となります。(下図「数の種類」参照!(^^)/ )
(→ ちなみに有理数・無理数は、英語だと rational・irrational number です。rationalは、日常では ”合理的な” などの意味ですが、数学界では有理数。「ratio (比・率) + -nal (接尾辞:~の・~な、といった意味の形容詞へ)」なので、即ち ”比な数”、つまり「整数比になる数・整数比ではない数」という見方です。この辺りからも、比と分数の密接な関係を感じられますが、”比と分数” については6年生で!)
それでは、先の①~⑤の分数の話に戻ります。まずは5つを改めてご紹介すると;
①分割分数、②量分数、③単位分数、④割合分数、⑤商分数
です。ところで、分数は上述の通り「数の表し方の一つ」、つまりは分数で表された数も「数」です。この5つも、①~④は分数特有なものではありません。これらの名称は「一般的な 数の捉え方や用いられ方の種類 だけど、その数が分数だった場合に、そう用いられている分数に付けられたネーミング」と言えます。(⑤はちょっと別。)
このような立派な名前が付いているため、これらは分数独特の考え方のことなのかな、と最初は誤解されやすいかもしれません(誤解したのは作成者だけかもしれません(笑))。(もちろん、名付け反対!などではありません。名前が付けば、この考え方の界隈を一単語で表せる、というメリットもありますし!)。
が、⑤以外、その捉え方や用いられ方は、慣れ親しんだ整数と同じです。この単元の、「分数が表す意味」について学ぶ一連の項目は、粗~くまとめると『「そもそも数って どういう場合に どう捉えて使うと どういう意味を表すんだっけ」をおさらいしつつ、「そのそれぞれの数、分数も数だから、分数使ってもいいからね!」と言っている 』だけの話です。
そして、上の①~⑤の順番は、子供達の理解しやすい順、即ち ほぼ習う順、が考慮された、学習指導要領に沿った順番ですが、大人なのでそこは無視して「より大きな意味」というカテゴリで括り直して;
- 「③単位分数」
- 「①分割分数・②量分数」
「—」
「④割合分数」 - 「⑤商分数」
とした方が捉えやすいと思います。ざっと解説していきますと;
「③単位分数」
他意のない「数という概念」の基本単位は、整数なら当然「1」です。分数の場合、1/2 や 1/3 などの 分子が1の分数が、それぞれ、その分母の分数の、数としての基本単位として捉えられます。分子が1の分数がこのように捉えられているとき、それらは「単位分数」と呼ばれます。(整数はその場合の1に特に名前はありません。)
「①分割分数・②量分数」
「—」
「④割合分数」
整数でもお馴染みの、数の三大使われ方「数量」「順序」「割合」なだけです。(が、算数・数学では「順序」に分数は 使わないので「—」としてあります。文学などで使えばファンタジー感が演出できたりもしますね☆) 分数がこの使われ方をした際の「そう使われている分数」のそれぞれの呼ばれ方です。
ここでちょっとややこしいのが、整数が「数量」として用いられるとき、「明確な1の基準のない数量(〇個や 〇枚 などの 数詞という言葉で数えられるもの)」も、「1となる基準量が厳密に単位として定められた物理量(〇cmや 〇L など)」も、どちらも「数量」であることは同じで一括り。ですが、分数だと前者が「分割分数」、後者が「量分数」と、何だか別物みたいに扱われること、かと思います。
(→ ④割合分数の詳細と、⑤商分数、は5年生で!)
分数の加法・減法
- 簡単な場合で、同分母の分数の加法・減法の意味や、計算の仕方について、理解できるようにする
(→ ここでの簡単な場合とは、分子が分母より小さい分数(真分数)同士で、和が1までとなる加法 およびその逆の減法、までです)
(→ つまり同分母で、足しても分子が分母を超えない程度まで)
(例:1/5m と2/5m を合わせる場合に、1/5+2/5 という式を立てられて、1/5mの三つ分(単位分数1/5の一つ分と二つ分を合わせて三つ分)として捉えて、答えが3/5mになることが理解できるようにする)
- 上記のような「簡単な同分母の分数の加法・減法」の計算を実際に行う
- 実際の計算を通して、計算ができるということからも、分数も整数と同じように「数」として見ることができるのだ、ということを再確認する
- 1という整数を、計算過程で、必要に応じて 10/10 や 2/2、3/3、… などとも見れるようにする
(例:2/10 + 8/10 の計算過程での 10/10 や、1−2/3 などの計算過程での 3/3 – 2/3 など )
(※ 最終的な答えになった場合は1に戻す)
(→ 有効数字の概念の学習は中学校なので、小学校の間は可能な限り簡潔に表現できるようにする) - 整数1には、表記として 1以外にも、10/10 があることの理解を固め、2/2、3/3、… などもあることを理解して、計算過程の必要に応じて使うことができるようにする
※ご注意事項
※ ご紹介する単元名や項目名は、学習内容の意味的なまとまりをご紹介するために、学習指導要領や子供達の教科書等を参考に、作成者が個人的にまとめたものです。学習指導要領や各教科書および参考書等での、実際の括り方や 用いられている名称とは 異なる場合もありますので ご了承ください。
※ 調査や要約等には 細心の注意を払い、出来る限り正確な内容となるよう努めていますが、あくまでも全て、個人の解釈です。内容を保障するものではありませんので、ご了承ください。
おわりに
以上で、3年生算数【数と計算】領域の5回目について、各項目の詳細説明は終了です。
大分続きましたが、3年生のこの領域には10単元ありますので(※ 当ブログでの括り方です)、領域内の項目説明はあと1回あります!もう一頑張りです!(^^)/
次回は、「小学校算数3年生の項目詳細【数と計算】⑥」です。
それでは(^^)/






