こんにちわ、訪問ありがとうございます!
はじめに
今回からついに、本題である「小学校の勉強内容」に入っていきます!
学習指導要領では、まず 目指すべき姿である目標が定められており、それに沿うように 具体的な学習内容が指示されていきます。
なので 本来なら まず目標を見ていった方がよいのでしょうが、あまり詳しく追い過ぎると かえって掴みにくくなる可能性もあり、かつ 時間もかかりすぎるので、当ブログでは 今回からは「具体的な内容」に絞って ご紹介していきます。
最初の教科は、ウリボー達の苦手な「算数」です、親心というか 親の焦りというか…(-_-;)
そして 各学年で習う内容を詳しく見ていく前に、まずは 小学校全体を通して学ぶことの、大きな流れを捉えたいと思います。
というワケで 今回は算数の初回、「小学校算数の内容領域と単元」となります。
では、見ていきましょう!
全体像と全体の流れ
算数の内容は、計算的なこと、図形的なこと、データ処理的なこと、など…と、その内部で大きく5つの領域(ジャンルのようなもの)に 分かれているので、まずそちらについて 簡単に解説します。
そのあとで、それぞれの領域ごとに、各学年で学習する内容を 単元名を列挙する形でご紹介します。


小学校算数の内容領域

小学校 算数の内容領域は「数と計算」「図形」「測定」「変化と関係」「データの活用」の5つで構成されています。
そもそも ここでの「領域」とは、ほぼ「ジャンル」や「分野」と捉えていただいて問題ありません。
※ 厳密には これらの単語には ニュアンスの違いや 正しい使い分けがあると思いますが、置いておいて…。
「ジャンル」や「分野」の方が 馴染みやすい言葉かとも 思うのですが、学習指導要領では「領域」と表現されていますので、ここは公式に合わせて進めたいと思います。
小学校 算数の内容は、大きな5つの領域で構成されています。
既に上に 結論はありますが、改めて、領域を展開します。
小学校 算数 5つの領域
- 数と計算
- 図形
- 測定 (1-3年)
- 変化と関係 (4-6年)
- データの活用
これはまさに領域展開! 某有名マンガが頭をよぎります、先生ファンです、女子なので(笑)
が、本題に戻りまして、各内容領域を もう少し 詳しく見ていくと、以下になります;
小学校 算数 の 各内容領域 … (超)概要
- それぞれ、算数や数学の主軸ともいえる 数・量・図形 についての内容であり、小学校における主要な学習対象である3つです (※数・量・図形というので この順番で指示してほしいな~ などとも思いますが、学習指導要領では学年ごとに 『 数=「数と計算」、図形=「図形」、量=「測定」』の順番で 指示されていきます)
- 数量の変化から そこにある「関係」という実体のないものを扱い「関係の姿」を把握すること、逆に「関係の姿」から変化後の値が分かること、さらにそれらを問題解決へと利用すること、という関数の基礎を学ぶ (※つまり「関数」の初歩と言えます)
- 事実であるデータを整理して データが語る真実を読み解く、そこから 不確実な事柄への考察へと応用させていく、という、データを扱い分析していくための手法や考え方 など の基礎を学ぶ (※つまり「確立・統計」の初歩と言えます)
次に これらを習う時期についてです。
まず 数・量・図形のうちの2つ、数と図形 である「数と計算」「図形」は、難易度をあげながら、全学年を通して学んでいきます。
数・量・図形の残り1つ、量に関する内容である 「測定 (1-3年)」は、低学年 1-3年生の学習内容となり、 量の概念の理解(時間など見えないものも含めます) と 測定の考え方および技術 を学びます。
「関係」という実体のないものを扱う「変化と関係 (4-6年)」は、概念的な内容になってくるので難易度があがるため、高学年 4-6年生で学びます。
(※中学で「関数」へと繋がっていく領域です。関数とはざっくりですが「定まった処理内容があって、処理内部の ある値を決めると その処理内容に従って 返る値も 決まった数が返ってくる その関係 」のようなものです。小学生はまだ関数ではなく「関係」として学びますが、実質は「関数の始まり」です。)
語るデータに挑む「データの活用」は、全学年を通して学びます。目茶苦茶な状態のデータからは何も分かりませんが、データは正しい手法で処理をしていくと 真実を語りだします。その「正しい手法」や「真実の読みとり方」を学びます。「手法」や「読みとり方」は 算数・数学的ですが「施した数学的処理・読み取った数学的意味 から 数学ではない意味を捉え、だからどうするか などの 数学ではないことを考えて、未来に活かす」ことこそが本当の目的の領域です。
(※もちろん学生時代が終われば、どの領域も 数学自体が目的で数学を使うことは 少ないと思いますが、この領域は 特にそのことが顕著に表れています。なので小学校のうちから 算数・数学の範疇を超えて「だからこの結果を 大きな目的のために どうするのか」を考えることも練習していきます。)

※もちろん、学習時期の定められている2つの内容領域も、時期外は無関係!なのではありません。1-3年生で学んだ量と測定の知識・技術はその先もずっと使います。むしろ使えることが大前提で、他の領域の主要な土台やツールとなっていきます。4-6年生から始まる「関係」という概念的な内容は、机上で理論を習えばいきなり理解できるものでもなく、理解の基礎となるような学びや経験が、低学年のうちから必要です。
※ 学習指導要領では「A 数と計算」、「B 図形」、「C 測定」(1-3年)および「C変化と関係」(4-6年)、「Dデータの活用」として 指示されています。
では、次に、この各領域ごとに学ぶ 具体的な単元を 一覧で見ていきましょう!
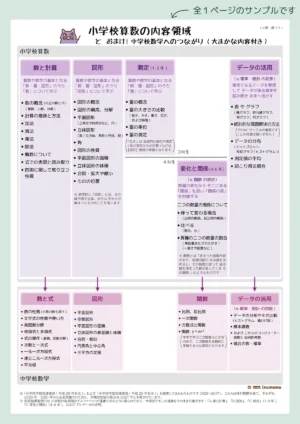
小学校算数の単元 (内容領域・学年ごと)
それでは、6年間の大まかな内容を「内容領域ごと」に「各学年」での単元を挙げる形で どんどん ご紹介していきます!
※ ご紹介する単元名は、学習内容の意味的なまとまりをご紹介するために、学習指導要領や子供達の教科書等を参考に、作成者が個人的にまとめたものです。学習指導要領や各教科書および参考書等での、実際の括り方や 用いられている名称とは 異なりますのでご了承ください。
数と計算
数と計算 : 各学年の単元
- 数の構成と表し方
- 整数の加法・減法
- 数の構成と表し方
- 整数の加法・減法
- 整数の乗法
- 分数について
- 整数の表し方
- 整数の加法・減法
- 整数の乗法
- 整数の除法
- 小数について
- 小数の加法・減法
- 分数について
- 分数の加法・減法
- 数量の関係を表す式
- そろばんを用いた数の表し方と計算
- 整数の表し方
- 整数の除法
- 小数について
- 小数の加法・減法
- 小数の乗法・除法
- 分数について
- 分数の加法・減法
- 概数について
- 数量の関係を表す式
- 計算に関して成り立つ性質
- そろばんを用いた数の表し方と計算
- 整数の性質と構成
- 小数点と 整数や小数の表し方
- 小数の乗法・除法
- 分数について
- 分数の加法・減法
- 数量の関係を表す式
- 分数の乗法・除法
- 数量の関係を表す式:文字を用いた表記
図形
図形 : 各学年の単元
- 身の回りのものの形
- 身の回りのものの位置
- 図形について
- 図形について
- 角の大きさ
- 平面図形
- 立体図形
- 平面図形の面積
- ものの位置
- 平面図形
- 立体図形
- 平面図形の面積
- 立体図形の体積
- 平面図形
- 平面図形の面積
- 立体図形の体積
- 概形と およその面積・体積
測定 (1-3年生)
測定 (1-3年生) : 各学年の単元
- 身の回りのものの大きさ
- 時刻
- 量の単位と測定
- 時刻と時間
- 量の単位と測定
- 時刻と時間
【4年生 】
【5年生 】
【6年生 】
変化と関係 (4-6年生)
変化と関係 (4-6年生) : 各学年の単元
【1年生 】
【2年生 】
【3年生 】
- 伴って変わる場合:そこにある関係
- 比べる:割合
- 伴って変わる場合:比例の関係
- 比べる:割合
- 異種の二つの量の割合:単位量あたりの大きさ
- 伴って変わる場合:比例の関係、反比例の関係
- 比べる:比
データの活用
データの活用 : 各学年の単元
- 数量の整理
- データの分析
- データの分析
- データの収集と分析
- データの収集と分析 および問題解決
- 測定値の平均
- データの収集と分析 および問題解決
- 起こり得る場合


おわりに
以上で、今回は終了となります。
このような流れで 小学校 算数は 進んでいくのですね!…と言われても、これだけでは よく分かりませんよね (^^;)
もっと詳しく見ていきましょう、ということで、次からは 各学年ごとに二回に分けて、今回ご紹介した単元の中の項目 および詳細説明を ご紹介していきます。
では 次回は1年生の一回目で「小学校算数1年生の単元と項目 」となります!
それでは(^^)/