こんにちわ、訪問ありがとうございます!
はじめに
前回の記事「小学校算数2年生の単元と項目」で内容一覧を、具体的には『 内容領域ごとの「単元名」「項目名」』をご紹介しました。
それだけでも十分かもしれませんが、学習指導要領 公式解説には、なるほど!と思う詳しい内容が沢山載っています。
家庭学習をサポートする上で、知っていて損はないと思います。よって今回から、公式解説を基にまとめた「項目の詳細説明」を、上記でご紹介した「項目名」に沿って 一覧にして ご紹介していきます。
一度にご紹介するとボリュームが多くなりすぎますので、領域ごとに記事を分けます。さらに、内部もボリューミーな領域は、1~3単元ずつに分けていきます!(特に【数と計算】は多いです(-o-;))
それでは今回は【数と計算】1回目、「小学校算数2年生の項目詳細【数と計算】①」です、見ていきましょう!
【数と計算】領域について

2年生の単元一覧
2年生で学習する【数と計算】領域の単元は、以下になります;
【数と計算】 – 単元一覧 :2年生
※ 左の番号は当ブログの領域内の記事番号です、算数的な意味等はありません。m(_ _)m
各単元の項目詳細
以下より、算数2年生の【数と計算】領域中の単元「数の構成と表し方」「整数の加法・減法」の各項目について、詳細を どんどん ご紹介していきます!
- 各単元ごとに「項目名」「項目詳細」が記載してあります
数の構成と表し方
- 必要に応じて、ものの個数を、同種や同数ずつの集まりにして数えられるようにする
(2・5・10 ずつなどでまとめて数える、ものの色や形などで分類して数える、など) - 同数ずつの集まりにして数える経験を通して、次のような、数のさらなる理解へとつなげていく;
- 同数ずつまとめて数えることで、乗法の意味の理解につなげていく
- 多くのものの個数を数えるときに、まず10ずつのまとまりを作り、さらにそれを10ずつのまとまりにして数えていくことで、桁数が大きくなった際の数の表記方法の理解につなげていく
- 4位数までの数の表し方と、それらの数の大小や順序を理解する
- 3位数から4位数へと、数の範囲を徐々に広げて理解を深める
- 数の表し方のルールを理解する
(10ずつまとまると位があがる、かつ、位が1つ上がるごとに左の位置に1つ進んで記載していくというルールのことで、この表し方を「十進位取り記数法」といいます) - 数の読み方との比較により、記数法の「空位となる位に0を書く」と言う特徴を理解する
(例えば、7000なら、読むときには空位ではない位だけを言うが、書くときには空位を表す0を各位に記入しておかなければならない) - 数の大小関係を、不等号「>」「<」を用いて表現できることを知る
- 9999 の次の数、などとして「10000、1万 」という数を知る
( ※「1万を超える数」の学習は3年生です)
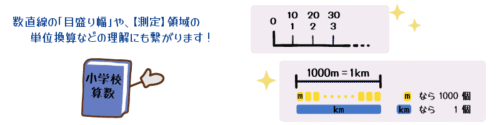
- 「十や百などを単位として数の大きさを捉えた場合、十や百がいくつ分になるのか 」という、数の相対的な大きさを理解する
(例えば、6000 なら、「10 が 600 個集まった数」とみたり、「100 が 60 個集まった数」とみたりする)
※ 相対的とは、他のものとの関係性や比較において成り立つ様子です
- 数の相対的な大きさを捉えることにより、数の仕組みについての理解を深めて、数の感覚を豊かにする
(4位数までの数の理解を通して、具体的な物を用いた活動も行い、桁の形式的な処理方法の暗記ではなく、数の相対的な大きさについての考え方を理解できるようにする)
- 一つの数を、他の数の積としても見ることができるようにして、数の乗法的な構成についても理解する
- ものの集まりをいくつかずつにまとめて数える活動を通して、数の乗法的な構成についての実感を深める
(例えば、12 個のおはじきを工夫して並べる、という活動を行い、12個は 2×6、6×2、3×4、4×3 と、いろいろな並べ方ができることを実感する、など) - 逆に、ある部分の大きさを元にして、「その幾つ分」として全体の大きさを捉えることができるようにする
- 数の乗法的な構成を捉えることにより、数についての理解を深めて、数の感覚を豊かにする
- 量や順序など、数が表す意味を再確認する
- 「物事を分類整理して、その結果を数を用いて表す」という考え方が、日常生活で多く使われていることを知り、身近な例などを 改めてその見方で再認識する (名簿番号・電話番号・ホテルの部屋番号・などなど )
- 数を用いて整理する利便性を知り、そのよさを理解する

整数の加法・減法
- 「2位数の加法 および その逆の減法」が、1位数などでの基本的な計算を元にして計算できることを理解する
→1年生で学習した 「1位数と1位数の加法と その逆の減法」および 「簡単な場合の2位数の加法と減法」を元にして、和と差を求めることができる
(例えば、「28 + 57 」なら「一の位同士を加えた 8+7= 15 」と「10 のまとまり同士を加えた 20 + 50 = 70 」とを合わせて「85 」と計算できる)
- 2位数の加法・減法の、筆算の方法を理解する
(「各位を揃えてかけば、2位数の計算が各位同士の数の計算になり、1位数の加法または減法の計算で処理できるようになること」と、「繰り上がりの考え方」を理解して、筆算を理解できるようにする )
- 「2位数の加法 および その逆の減法」の計算が、確実にできるようにする
- 「加法と減法の相互関係」を理解する;
- 「A と B を合わせると C になる 」という関係の時、「C を求める場合が 加法 A + B = C 」で、「A や B を求める場合が減法 C - B = A および C - A = B 」というお互いの関係を、図および実際の数で理解する
※ このとき加法と減法は、三つの数量 A・B・C のどれを求めるかによって 相互に関係付けられており、このような関係を 「加法と減法との相互関係」といいます
- 具体的な場面に当てはめて、A・B・C それぞれを求めることができるようにする;
- 例えば、8個のリンゴがあって4個もらったから12個になったとき、8(A) + 4(B) = 12(C) について
① C を求める (8個あって4個もらったらいくつか)
② A を求める (いくつかあって4個もらったら12個になった、もとはいくつあったのか)
③ B を求める (8個あっていくつかもらったら12個になった、いくつもらったのか)
の 各場合が全て求められる

- 分からない数を一旦”□”とする、という方法を用いて計算が行えることを知る
- 意味がまとまっている、または先に計算するとラクになる、などの理由で「先に計算を行いたい部分を 括弧 ″()″ でくくる」という方法を用いて計算が行えることを知る
- これらの方法を用いて計算を行う
(ここ以外の単元や項目の学習時にも必要に応じて用いる)

- 見積もる、という考え方を知る
(「計算結果の数が 大体どのくらいの大きさやケタ数になりそうか」を計算前に予想してみる、という発想自体や、先に考えておくことの利点を知る)
(※「見積もる」という言葉はまだ学びません、「いくつぐらいになるかな」などの表現に導かれて、計算前に予想してみることになるかと思います) - 計算結果の見積もりを 気に掛けてみる
(ここ以外の単元や項目の学習時にも必要に応じて考えてみる)
- 計算には、「法則」として成り立つ性質があることを知る
(小学校では「法則」ではなく「きまり」と表現されていることが多いです)
(「法則」という名前はついていない性質もあり、例えば 4年生で学習する 「除法で成り立つ性質 (被除数・除数に同じ数を掛けても商は同じ)」なども、法則とは呼ばれませんが 性質です、ややこしい(笑))
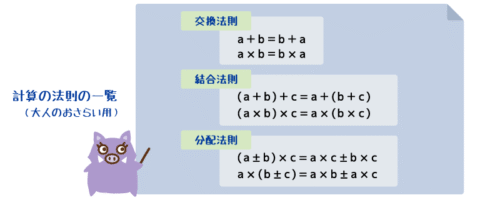
- 加法の計算で成り立つ性質である「加法の交換法則」と「加法の結合法則」を知り、それぞれの法則を具体的な数を用いて確認することで、これらの法則が確かに成り立つことを実感する;
- 加法の交換法則(足し算の交換のきまり )
→ 項を入れ替えても計算結果は同じになる
(足される数と足す数の順番を入れ替えて足しても答えは同じになる ) - 加法の結合法則(足し算の結合のきまり)
→ 先に計算しておく結合の組み合わせを変えても計算結果は同じになる
(3つ以上の足し算で、前から順に足しても 後ろを先に足しておいても答えは同じになる)
- 加法の結合法則や交換法則を活用して、「計算の確かめ」をしてみる
( 加法の交換法則を活用して「8+16」と「16+8」の結果を比べて確かめる、など) - 加法の結合法則や交換法則を活用して、場合によっては 二つの法則を組み合わせるなどして、計算の仕方を工夫したり、新しい計算の仕方を生み出したする
(一の位を足して10になる数の組み合わせに着目して、それらをまとめて 計算を効率的にする、など ( 3+6+17= 6+3+17= 6+ (3+17) = 26 など ) ) - 加法の結合法則や交換法則を 計算の確かめや工夫に活用することを通して、これらの法則は、覚えることが目的ではなく、「活用するもの」であることに気付く
(もちろん、ここで学ぶ加法の法則のみではなく、乗法で成り立つ法則も、法則として命名されていない性質も含め、「計算に関して成り立つ法則や性質」は、覚えるためのものではなく、「活用するもの」です) - 法則を利便性のために活用しよう、という考え方と姿勢を育む
- 次のような簡単な3位数の加法・減法を行いながら、計算の仕方についての理解を一層深める;
(2位数の加法 および その逆の減法の計算方法や、今までの学習で学んだ数の考え方の知識を基にして行う)
- 百を単位としてみられる数の加法・減法
(300+200 や 800−500 のような、一・十の位が共に 0 の3位数同士の計算)
( → 百を単位とした数の見方に関連させて、3+2 や 8−5 を元にして求めることができるようにする) - 3位数と2位数との加法・減法で、百の位への繰り上がりや百の位からの繰り下がりのないもの
- このような簡単な3位数の加法・減法の計算を知ることで、「2位数までの計算の理解」と「3位数までの数の理解」を、より確実なものにしていく
※ご注意事項
※ ご紹介する単元名や項目名は、学習内容の意味的なまとまりをご紹介するために、学習指導要領や子供達の教科書等を参考に、作成者が個人的にまとめたものです。学習指導要領や各教科書および参考書等での、実際の括り方や 用いられている名称とは 異なる場合もありますので ご了承ください。
※ 調査や要約等には 細心の注意を払い、出来る限り正確な内容となるよう努めていますが、あくまでも全て、個人の解釈です。内容を保障するものではありませんので、ご了承ください。
おわりに
以上で、2年生算数【数と計算】領域の1回目について、各項目の詳細説明は終了です。
2年生のこの領域には4単元ありますので(※ 当ブログでの括り方です)、領域内の項目説明は続きます!
次回は、「小学校算数2年生の項目詳細【数と計算】②」です。
それでは(^^)/