小学校算数３年生の項目詳細【数と計算】②

こんにちわ、訪問ありがとうございます！

はじめに
【数と計算】領域について
３年生の単元一覧
各単元の項目詳細
- 整数の乗法
- ※ご注意事項
おわりに

はじめに

前々回の記事「小学校算数３年生の単元と項目」で内容一覧を、具体的には『内容領域ごとの「単元名」「項目名」』をご紹介しました。

小学校算数３年生の単元と項目

算数３年生で学ぶ内容について「単元名」ごとに「項目名」「捉え方・考え方などのポイント」「用語や記号」を紹介しています。

それだけでも十分かもしれませんが、学習指導要領公式解説には、なるほど！と思う詳しい内容が沢山載っています。

家庭学習をサポートする上で、知っていて損はないと思います。よって前回から、公式解説を基にまとめた「項目の詳細説明」を、上記でご紹介した「項目名」に沿って一覧にしてご紹介しています。

一度にご紹介するとボリュームが多くなりすぎますので、領域ごとに記事を分けています。さらに、内部もボリューミーな領域は、１～３単元ずつに分けています！（特に【数と計算】は多いです(-o-;)）

それでは今回は【数と計算】２回目、「小学校算数３年生の項目詳細【数と計算】②」です、見ていきましょう！

PDFとnoteのご案内

〇内容一覧である上記の記事を、見やすく印刷しやすいようA4にまとめた「小学校算数３年生の単元と項目 PDF」を noteで公開予定です！(有料公開です)

→ PDFは現在準備中です、完成次第こちらでサンプルとともにご案内します、よろしくお願いします m(_ _)m

【数と計算】領域について

【数と計算】領域では、算数や数学の基本となる「数・量・図形」のうち、「数」について学びます。

および数を操作するための「演算」や「演算子を用いた式」などの意味・ルール・使い方、等も学びます。

３年生の単元一覧

３年生で学習する【数と計算】領域の単元は、以下になります；

【数と計算】 – 単元一覧：３年生

「整数の表し方」
「整数の加法・減法」
　⇒ 別記事です：該当記事へ
「整数の乗法」
　⇒ ★当記事です★（タイトルでジャンプ）
「整数の除法」
　⇒ 別記事です：該当記事へ
「小数について」
「小数の加法・減法」
　⇒（※ 記事準備中です）
「分数について」
「分数の加法・減法」
　⇒（※ 記事準備中です）
「数量の関係を表す式」
「そろばんを用いた数の表し方と計算」
　⇒（※ 記事準備中です）

※ 括り方や単元名は当ブログの場合です、学習指導要領や教科書等とは異なることもあります。
※ 左の番号は当ブログでの領域内の記事番号です、算数的な意味等はありません。m(_ _)m
※ 準備中の記事については、今後記事の分け方が変更になる可能性もあります。

各単元の項目詳細

以下より、算数３年生の【数と計算】領域中の単元「整数の乗法」の各項目について、詳細をどんどんご紹介していきます！

各単元ごとに、「項目名」「項目詳細」が記載してあります

※ ご注意事項も下部にございますので、ご一読ください。

整数の乗法

整数の乗法 – 項目詳細 : ３年生【数と計算】

● 「２位数や３位数×１位数や２位数」の乗法について

まず、数をいつもの「１」を単位ではなく「10」を単位（１まとまり）として捉えることにより、「被乗数（掛けられる数）を10倍すると積も10倍になる」という乗法の性質を理解する
（例：５ × ３＝15 だが、被乗数を 10倍にすると 50 ×３＝150 で積も 10倍になる）
（※ 等式の性質としての、乗法の性質である「a＝b ならば ac＝bc」が成り立っていますが、この性質の学習は中学１年生です）
そして乗数（掛ける数）が１位数の計算の場合には、被乗数（掛けられる数）を位ごとの数のまとまりに着目すると、基本的な計算を基にして計算できるようになることを理解する
（例：25 ×３ならば、25 は 20 ＋５と捉えて、20 × ３＋５ × ３で計算できる）
次に、乗数（掛ける数）が２位数の計算の場合は、十の位を掛ける計算と、一の位を掛ける計算を基にして、計算できることを理解する
（例：25 × 43 ならば、乗数（掛ける数）の 43 を 40＋３と捉えて、25 × 40 ＋ 25 × ３となり、乗数（掛ける数）が１位数の計算を基にして求めることができる）
（乗数の十の位の計算 25 × 40 については、40を十を単位として４つ分、つまり一旦４として計算して、計算後にその単位をもとの数の 10　に戻す（つまり10を掛ける））
被乗数が３位数になっても、同様の考え方を拡張させて計算できることを理解する

これは分配法則を活用した計算方法であり、筆算の仕方に結び付く

● 計算結果の見積り … 簡単な乗法（「２位数×１位数」程度）の暗算を用いて

乗法の計算結果の確認にも、「見積り」を生かす
（例：19 ×５なら、これを計算する前に「19は大体 20 なので、20×５＝100 となるから、19に戻して計算すると100よりは小さくなるな」と予想してみる、など）
見積りを行うに当たって、「２位数 × １位数」程度の簡単な乗法を、暗算でできるようにする

● 「２位数や３位数×１位数や２位数」の乗法の筆算

上記の計算の考え方から、まずは乗数（掛ける数）が１位数の場合を基に、筆算の仕方を理解して、練習する

● 計算力の確実な習得 … 「２位数や３位数×１位数や２位数」の乗法（および、整数での乗法の計算力ひとまず完成）

「２位数や３位数 ×１位数や２位数」の乗法の計算を確実に出来るようにする
ここまでで整数の乗法の計算力を確実に習得して、その力を整数はもちろん、次の４年生から学んでいく小数の乗法、および６年生から学ぶ分数の乗法の計算への土台ともする

● 乗法の計算の適切な利用

被乗数（掛けられる数）や乗数（掛ける数）は、人数・個数・長さ・重さ・値段、と様々な場合があるが、どのような状況でも乗法が用いられる場面を判断して、必要な際に適切に用いることができるようにする
（※ ただし「数量」でも「順序」でもない「割合（別名”率”）」という数については、〇倍の〇という数なので、乗数としては出てきていますし使えるようにしますが、「被乗数が割合（別名”率”）」を扱うのは、５年生からです。）
除法の学習が同じく３年生から始まるが、除法の学習後は、除法の逆算としての乗法の問題も理解できるようにする
（例：ひもを５等分した一つ分が10cmだった場合、はじめのひもの長さは何cmか、など）

● 乗法で成り立つ性質 … 乗数が１ずつ増えるときの積の増減や、交換法則・結合法則・分配法則と成り立つことの確認

２年生で学習した「乗数（掛ける数）が１ずつ増えるとき積は被乗数（掛けられる数）の大きさ分ずつ増える」という様子を基に、「乗数が１ずつ増減するとき積は被乗数の大きさずつ増減する」ことについて、成り立つことを調べて確認する
（→ a × b で、b が１ずつ増減するときに積が a ずつ増減する様子は、分配法則の式からも分かる； a ×（ b ±１）＝ a × b ± a × 1 ＝ a × b ± a ＝（ a × b ）± a ）
乗法について、交換法則・結合法則・分配法則が成り立つという考え方を理解して、確かに成り立つことを調べて確認する
（→ 計算に関して重要な交換法則・結合法則・分配法則の３つの性質は下記になり、そのうち乗法に関するものの「考え方」が成り立つことを理解します）
（※ これらを「法則（きまり）」として学習して一般化して理解をまとめるのは４年生、これらの法則含めた性質が小数も含めて成り立つことについて理解できるようにするのは５年生です）

● 乗法で成り立つ性質の活用

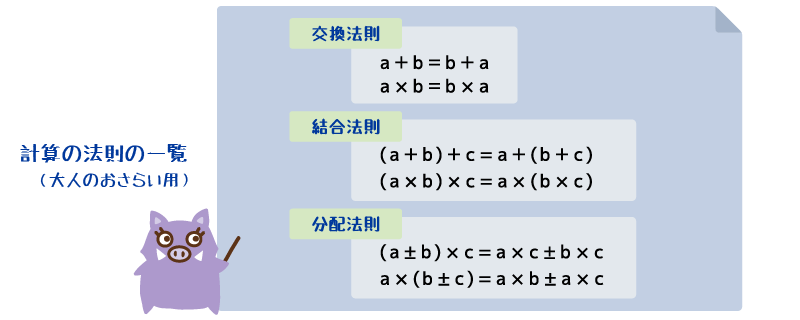
「乗数が１ずつ増減するときの積の増減」や「交換法則・結合法則・分配法則」を様々に活用して、乗法の計算の仕方を考えたり、計算の工夫や確認を行ったりする；

例１：「乗数が１ずつ増減するとき積は被乗数の大きさずつ増減する」性質を活用して、積を忘れてしまった九九を、周りの九九の積から思い出す
（→ 七六を忘れてしまったが、七五35は覚えているので、35＋7＝42 より、七六42を思い出せる）
例２：分配法則「 a ×（ b ± c ）＝ a × b ± a × c 」という性質が成り立つことを実際の数で調べ、この性質は筆算で計算する際などに既に用いてきていること、を改めて理解する
例３：４×７×25 について、そのまま計算した場合は、まず４×７＝28 を計算し、その後 28 × 25 を計算しないといけないが、工夫して計算すると、まず交換法則を用いて４×７× 25 を７×４× 25 として、次に結合法則を用いて７×（４× 25 ）＝７× 100 ＝ 700 とすることができ、積が簡単に求められる

● ０の入る乗法

乗法の意味「一つ分の数（被乗数）× 幾つ分（乗数）＝全体の数（積）」において、被乗数が０の場合、および乗数が０の場合、の意味を理解する；

① 被乗数が０の場合
：「一つ分の数が０」のものが幾つあっても０になる
（例：「飴玉が全く入っていない袋」が３袋あっても、飴玉の数は０ →「０× ３＝０」）
（→ 乗法の意味に戻り、０+０+０＝０とも求められる）
② 乗数が０の場合
：一つ分の大きさが幾つであっても「幾つあるかが０」なら０になる
（例：飴玉３個入りの袋がどこかにあったとしても、「その袋自体がここに全くない」ならば、ここの飴玉の数は０ →「３×０＝０」）
（→ ３×０の答えは、具体的な状況から０と考えたり、乗数が１ずつ増減する時の積の増減の性質を使って、３×３＝９、３×２＝６、３×１＝３と並べると積が３ずつ減っていくことから、３×１＝３の積から３を引いて３×０＝０と求められる、ということに気付けるようにする）