こんにちわ、訪問ありがとうございます!
はじめに
前々回の記事「小学校算数2年生の単元と項目」で内容一覧を、具体的には『 内容領域ごとの「単元名」「項目名」』をご紹介しました。
それだけでも十分かもしれませんが、学習指導要領 公式解説には、なるほど!と思う詳しい内容が沢山載っています。
家庭学習をサポートする上で、知っていて損はないと思います。よって、公式解説を基にまとめた「項目の詳細説明」を、上記でご紹介した「項目名」に沿って 一覧にして ご紹介しています。
一度にご紹介するとボリュームが多くなりすぎますので、領域ごとに記事を分けています。さらに、内部もボリューミーな領域は、1~3単元ずつに分けています!(特に【数と計算】は多いです(-o-;))
それでは今回は【数と計算】2回目、「小学校算数2年生の項目詳細【数と計算】②」です、見ていきましょう!
【数と計算】領域について

2年生の単元一覧
2年生で学習する【数と計算】領域の単元は、以下になります;
【数と計算】 – 単元一覧 :2年生
※ 左の番号は当ブログの領域内の記事番号です、算数的な意味等はありません。m(_ _)m
各単元の項目詳細
以下より、算数2年生の【数と計算】領域中の単元「整数の乗法」「分数について」の各項目について、詳細を どんどん ご紹介していきます!
- 各単元ごとに「項目名」「項目詳細」が記載してあります
整数の乗法
- 「一つ分の大きさ」が決まっているときに、「そのいくつ分かに当たる大きさ」を求める場合、加法でも表現できるが、「乗法」という求め方が用いられることを知る;
- 「3個のまとまり」が4袋分あることを、足し算(加法)で表現する
→ 3 + 3 + 3 + 3 - 1つずつの袋から 同時に1個ずつ取り出して数えると、一回数えるごとに4個となり、それが3回分と捉えることもできるので、それを足し算で表現する
→ 4 + 4 + 4
(ちょっと不自然な数え方ですが)
- 「3個のまとまり」を先に書き、それが4袋分あることを示す「×4」を後ろに書く、という「掛け算(乗法)」で表現する
→ 3 × 4
- 乗法は「 一つ分の数 が 幾つか ある場合の 全ての数 」を簡潔に求められる計算であることを理解する
- 乗法の式の書き方は 「一つ分の数」を先に書くことを知る
(日本の場合です)
- 「 一つ分の数(一つ分の数量の大きさ) × 幾つ分 = 全ての数(その幾つ分にあたる数量の大きさ)」であると捉える;
- 「 一つ分の数:1袋に3個ずつのアメ玉 」× 「 幾つ分:4袋分 」=「 全ての数:全てのアメ玉の数 」
→ 3 × 4 = 12

- 「幾つ分」ということを、上記のように 「掛ける数側の数量が幾つあるのか」という 「二種類目の数量」に着目した見方ではなく、「 もととなる一つ分の数 の 幾つ分にあたるという関係 なのか」という着目点に変えた捉え方にすると、掛ける数は、数量を意味しない「〇倍」という種類の数になることを知る
(この時、乗数(掛ける数)が意味しているのは、数量ではなく、「被乗数(掛けられる数) と積との関係」であり、この数、〇倍の〇という数を「割合 (別名”率”) 」といいます)
※ 子供達はまだ意識しませんが、ここが、小学校算数の最大の関門の一つ「割合」の初登場シーンです
- この時、「幾つ分」ということは「何倍」と表現することを知る
- 乗法は「 一つ分の数量の大きさ の 何倍にあたる数量の大きさ 」 を求めるということでもある、という意味も併せて理解する
- 「一つ分の数:3個のアメ玉」「の何倍:4倍」=「全ての数:全てのアメ玉の数 」
→ 3 × 4 = 12
- 乗法が用いられる具体的な場面を「 × 」の記号を用いた式に表す、逆に式から状況を読み取る
- 「掛ける数(乗数)が1増えると、積は掛けられる数(被乗数)分だけ増える」という乗法の性質を理解する
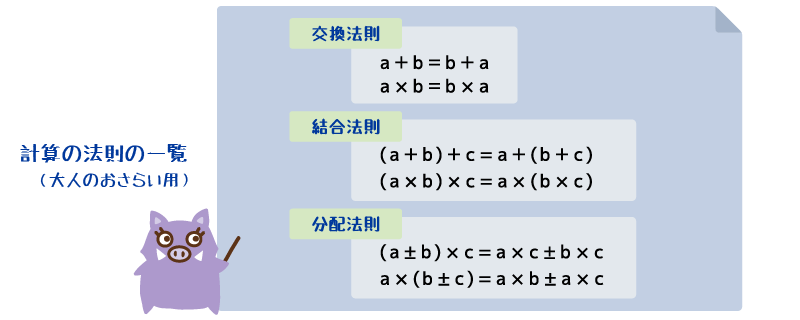
- 乗法の計算で成り立つ性質である「乗法の交換法則」を知り、具体的な数を用いて確認することで、この法則が確かに成り立つことを実感する
(乗法の結合法則や分配法則に基づいた考えに触れるかどうかは、各学校や先生に任されています)
(※3年生で「乗法で成り立つ性質」を学ぶ際は、乗法の法則(きまり)である 交換法則・結合法則・分配法則 の全てを同じように学習します。 4年生で「四則計算で成り立つ性質」を学ぶ際は、加法、減法、乗法について成り立つ法則(きまり) を ○・△・□ などの記号を使って一般化して表し、整理して理解します。)
- 九九を知り、その計算の意味と仕組みを理解する

(ダウンロードは無料です(^^)/)
- 九九を理解した上で暗記して、「1位数 ×1位数」の乗法の計算を確実に出来るようにする
- 九九の構成や観察を通して、乗法で成り立つ性質が九九でも成り立っていることに気付いたり、他にも様々な性質を見付け出したりする ;
- 九九でも「掛ける数(乗数) が1増えると、積は掛けられる数(被乗数) 分だけ増える」という乗法の性質が成り立っていることに気付く
(3の段なら 答えは3ずつ増えていく、など) - 九九でも 「乗法の交換法則」が成り立っていることに気付く
(3×7と7×3はどちらも 21、など) - ある九九を忘れたりした場合でも、乗数が1増えれば 積は被乗数分だけ増える性質や、乗法の交換法則を用いて、知っている九九を手掛かりにして 積を再構成できることに気付く
- 九九表では、同じ数同士を掛ける計算は 斜めに並んでいることに気付く
- 九九の表や図をもとに、ある段と別の段の掛けられる数(被乗数) 同士 および 積同士を足すと、掛けられる数(被乗数) を足した数の段になることに気付く
(例えば2×4=8 と3×4=12 で 被乗数同士・積同士を足すと 5×4=20 で 5の段の答えになる、乗数がいくつでも この性質が成り立つ、つまり 2の段と3の段の和は5の段になる)
(乗法の分配法則 (「a × ( b ± c ) = a × b ± a × c 」「( a ± b ) × c = a × c ± b × c 」) が成り立っています (この法則の正式な学習は3年生です) )
- 簡単な「2位数 ×1位数」の乗法の計算方法を知る
(12 程度までの2位数を用いて、「九九を基に、乗数が1ずつ増えるときの積の増え方で説明できる」ということを理解する)
分数について
- 元の大きさや量などについて、等分(半分や三等分などなど)した状態などを表すことができる『「分数」という 数の表し方』の存在を知る
(この表し方の存在を知ることがメインです、2年生では主に分子が1の状態で学習していき、また「分子・分母」などの用語は3年生の学習となります)
- 折り紙やテープなどを使って 1/2、1/3 などの簡単な分数を体感する
- 1/2 をさらに半分にすると 1/4 になることなどを体感する
- このような実際の物を操作する活動を通して、これらの数が「分数」と呼ばれる数の表し方であることを知り、実感を深める
- おはじきなどの実際の物を用いた 「全体の 1/2・1/3・1/4 などの大きさをつくる」活動を通して、数の乗法・除法的な見方の素地となる感覚をつくる;
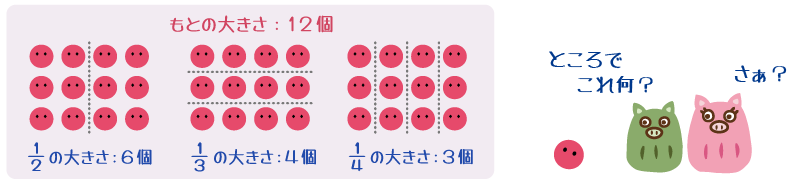
- 12個のおはじきを6個ずつや4個ずつなどに分け、それぞれ元の大きさと比べて、6個は「12個の半分の大きさ(1/2)」、4個は「12個を三つに分けた一つ分の大きさ(1/3)」、3個は「12個を四つに分けた一つ分の大きさ(1/4)」であることを確認し、また、このような表現で表せるようにする
- 同じ状況でも見方を変えると、12個は「6個の2倍」であり、「4個の3倍」であり、「3個の4倍」とも見られることを理解する
- つまり、例1とは逆に、『「元の大きさの 1/2 や 1/3 の大きさ」側を基準』にして『「元の大きさ」へ戻す』ことを考えると、12 個は「6の2倍の大きさ」、「4の3倍の大きさ」という見方になることを知る
- 「aの大きさの 1/2 がbの大きさ」「aの大きさの3倍が c の大きさ」などという場合に、1/2 や3倍という言葉だけでは、bや c の具体的な大きさは分からないことを知る
- つまり、bや c の具体的な大きが分かるためには、もととなるaの大きさをはっきりさせる必要がある、ということを知る
(例えば、同じ2倍でも、もとの数が5か 50 かで結果が全く違う数となることを確認する、などの具体的な数で、例を通して実感する)
(上記を式にすると「a × 1/2 = b」「a × 3 = c 」です。この時の 1/2 や3は「割合(別名”率”)」という数です。これは『「aとb」または「aとc」の間にある「関係」』を表す数なので、この数だけで「具体的な大きさ」は表せません。)
※ご注意事項
※ ご紹介する単元名や項目名は、学習内容の意味的なまとまりをご紹介するために、学習指導要領や子供達の教科書等を参考に、作成者が個人的にまとめたものです。学習指導要領や各教科書および参考書等での、実際の括り方や 用いられている名称とは 異なる場合もありますので ご了承ください。
※ 調査や要約等には 細心の注意を払い、出来る限り正確な内容となるよう努めていますが、あくまでも全て、個人の解釈です。内容を保障するものではありませんので、ご了承ください。
おわりに
以上で、2年生算数【数と計算】領域の2回目について、各項目の詳細説明は終了です。
および、今回でこの領域が終了となります!
が、各学年とも、学ぶ領域は4つずつありますので、項目説明は続きます。
次回は次の領域、「小学校算数2年生の項目詳細【図形】」です。
それでは(^^)/






