こんにちわ、訪問ありがとうございます!
はじめに
前回の記事「小学校算数3年生の単元と項目」で内容一覧を、具体的には『 内容領域ごとの「単元名」「項目名」』をご紹介しました。

それだけでも十分かもしれませんが、学習指導要領 公式解説には、なるほど!と思う詳しい内容が沢山載っています。
家庭学習をサポートする上で、知っていて損はないと思います。よって今回から、公式解説を基にまとめた「項目の詳細説明」を、前回ご紹介した「項目名」に沿って 一覧にして ご紹介していきます。
一度にご紹介するとボリュームが多くなりすぎますので、領域ごとに記事を分けます。さらに、内部もボリューミーな領域は、1~3単元ずつに分けていきます!(特に【数と計算】は多いです(-o-;))
それでは今回は【数と計算】1回目、「小学校算数3年生の項目詳細【数と計算】①」です、見ていきましょう!

【数と計算】領域について

3年生の単元一覧
3年生で学習する【数と計算】領域の単元は、以下になります;
【数と計算】 – 単元一覧 :3年生
※ 左の番号は当ブログでの領域内の記事番号です、算数的な意味等はありません。m(_ _)m
各単元の項目詳細
以下より、算数3年生の【数と計算】領域中の単元「整数の表し方」「整数の加法・減法」の各項目について、詳細を どんどん ご紹介していきます!
- 各単元ごとに、「項目名」「項目詳細」が記載してあります
整数の表し方
- 「万」の単位を知る
- 1万という数を様々な見方で捉えられるようにする
- 1万という数の大きさを実感的に捉えられるようにする
(1000が10個集まった大きさ、9999 より1大きい数、5000と5000を合わせた数、100の100倍、など) - 1万より大きいケタの数について、万を単位として、十・百・千を用いて「十万・百万・千万」で表せるようにする
- それらの数を、万の単位の目盛の付いた数直線の上でも理解できるようにする
- それらの数の大きさの大小を、不等号を用いて表せるようにする
(その際に「数直線」「等号」「不等号」という用語も正式に学習する)
- 十・百 のみではなく、千・万を単位として、「もとの数の大きさを捉えた場合 いくつ分になるのか」という 相対的な大きさを捉えられるようにする
(例えば、600000(60万)なら、「1000 が 600 個集まった数」と捉えたり、「10000 が 600個集まった数」と捉えたりできるようにする)
※ 相対的とは、他のものとの関係性や比較において成り立つ様子です - 「万を単位とした相対的な大きさ」を捉えて、前項目の十万・百万・千万 の意味を理解する
- 数の範囲が大きくなっても、このような相対的な大きさについて、2年生で学んだ捉え方と同じ考え方を拡張させて対応させて、「数の相対的な大きさ」についての理解を より深められるようにする
(2年生では、「十や百などを単位として数の大きさを捉えた場合、十や百がいくつ分になるのか 」という、数の相対的な大きさの捉え方を学びました) - 数を相対的な大きさで捉えることを生かして、大きな数の大きさを 実感的につかむ
(例えば、「10000kg(10t)の重さは、体重がおよそ1000kg(1t)の象(=2~3 才の若いアジアゾウくらい)が10 頭分」などとして 実感的に捉える)
( ※ 万を超える大きさの数になってくると、その大きさを”直接”実感することは 難しくなってきます ) - このような数の相対的な見方を活用して、一つの数を捉えるだけではなく、二つ以上の数の大きさを比較したり、計算の仕方を考えたりできるようにする;
- 例1:500 や700 は百を単位とすると、それぞれ5や7とみられるので、500 + 700 の計算は5+7とみることが出来る
(→ 3位数や4位数の加法・減法の計算の仕方につながる) - 例2:800 は百を単位とすると、8とみられるので、800 ×5の計算は、8×5とみることができる
(→ 2位数や3位数の乗法の計算の仕方につながる)
- 整数を10倍・100倍・1000倍 した大きさの数について調べる
- 10倍・100倍・1000倍 しても 数字の並び方は変わらないことに気付く
- 「もとの数」と「10倍・100倍・1000倍 した数」とで、「同じ数字に対応する位(十・百・千など)の数」は、それぞれ 10倍・100倍・1000倍にした位の関係になっていること、に気付く
(例:もとの数 25 と 10倍した数 250 について、「2」はもとの数では十の位の数だったが、10倍した後では、「十」を10倍した「百」の位の数になっている ) - 「もとの数」と、「10倍・100倍・1000倍 した数」を、『十・百などを単位とする数』と『もとの数で単位とした数を それぞれ 10倍・100倍・1000倍 した数』を 単位として、相対的な大きさを捉えてみる
(例:もとの数 60 では 十を単位として相対的な大きさを捉えると「十が6個」、100倍した数 6000 では「十」を100倍した「千」を単位として相対的な大きさを捉えると「千が6個」となる ) - このことから、「もとの数」と「10倍・100倍・1000倍 した数」について、数字の並び方は変わらないことや、同じ数字に対応する位(十・百・千など)の数は それぞれ 10倍・100倍・1000倍にした関係になることを 理解する
- 整数を10倍・100倍・1000倍 などにする操作を通して、もとの数との違いを比較してみたり、倍にしたあとの大きさを相対的に捉えたりする;
- 例1:234 を10 倍すると「百の位の2→ 千の位へ」「十の位の3→ 百の位へ」「一の位の4→ 十の位へ」と移る、という関係を見つけ出す
- 例2:234 を100 倍すると23400となり、万の位が2となることから、まずは大きく 2万代の数であることを捉える
(数を相対的な見方で捉えることで、倍にしたあとの数の大きさのおよそを掴む)
- 整数を 1/10 倍した大きさの数について調べる
- 10倍・100倍・1000倍 した時と同様に、 1/10 倍しても、数字の並び方は変わらないことに気付く
- 10倍・100倍・1000倍 した時とは逆に、もとの数と 1/10 倍した数とでは、同じ数字に対応する位(十・百・千など)の数は、それぞれ 1/10 倍した位の関係になっていること、に気付く
- 「もとの数」と「1/10 倍した数」を、『十・百などの単位とする数』と『もとの数で単位とした数を 1/10 倍した数』を単位として、相対的な大きさを捉えてみる
(例:もとの数 6000 では 千を単位として相対的な大きさを捉えると「千が6個」、1/10倍した数 600 では「千」を1/10倍した「百」を単位として相対的な大きさを捉えると「百が6個」となる ) - このことから、「もとの数」と「1/10 倍した数」について、数字の並び方は変わらないことや、同じ数字に対応する位(十・百・千など)の数は 1/10 倍した関係になること を理解する
- 99999999の次の数、などとして「100000000、1億」と言う数を知る
(※「1億を超える数」の学習は4年生です)
整数の加法・減法
- 3位数や4位数の加法・減法が、2位数などについての基本的な計算を基にして出来ることを理解する
- 2年生で学習した2位数および簡単な3位数の加法・減法 を基にして 和と差を求めることができる
(例:154+172 なら、一の位同士を加えた4+2=6と、十の位(10のまとまり)同士を加えた 50+70=120、そして これらと同様に、百の位(100のまとまり)同士を加えた 100 + 100 = 200 (と繰り上がり分)を合わせて 326と計算できる)
- 計算結果の見積もりに触れ、計算方法の検討や結果の確認に見積りを生かす
- 3位数や4位数と位が多くなってくると、位の揃え間違えによる計算間違いの可能性も上がってくるが、計算前におよその数を見積もっておくと、このような時にすぐに気が付けるようになる
(例:389 + 4897 の計算で、位を揃えずに計算し 8787 と答えを求めた場合、「389 は およそ 400」「4897 は およそ5000」とみれば 答えは「およそ 5400」になるので、大きく異なる 8787 という答えが間違っている、と気付ける)
(※「見積もり」という用語をいつ習うかの指示はありませんが、2年生では「計算前に結果を予測してみる」という考え方の練習に留まり、ここ3年生で 『それを「見積もり」と呼ぶ』 ことを学ぶ、という流れが多いかと思います)
- 見積もるに当たって、2位数同士の加法やその逆の減法程度の、簡単な計算を暗算でできるようにする
(これらの簡単な計算は、乗法や除法の計算を行う過程でも必要になる。また、日常生活でも多く用いられ、暗算で結果の見当を付けることも多い。そのような活用の仕方に触れ、つなげていけるようにする。)
- 2年生で学習した2位数の加法・減法の筆算の仕方を基に、3位数や4位数の加法・減法でも、位を揃えて筆算により計算できるようにする
- 3位数や4位数の加法・減法の計算を確実に出来るようにする
- ここまでで整数の加法・減法の計算力を確実に習得して、その力を整数はもちろん、同じく3年生から学んでいく小数および分数の加法・減法の計算への土台ともする
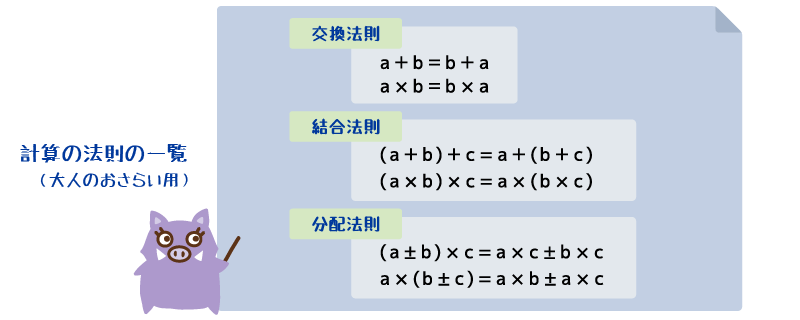
- 2年生で学習した「計算に関して成り立つ性質(加法の交換法則・結合法則)」について、3位数や4位数に 数の範囲を広げて考える
- これらの法則を生かして、幾つかの数をまとめたり、順序を変えたりすると 計算を能率的にすることができるので、これらを 計算の工夫や確かめに活用していく
- 加法・減法の計算が必要になるのは、人数・個数・長さ・重さ・値段 の計算、や順序の計算、と様々な場合があるが、どのような状況でも、加法・減法が用いられる場面を判断して、必要な際に適切に用いることができるようにする
※ご注意事項
※ ご紹介する単元名や項目名は、学習内容の意味的なまとまりをご紹介するために、学習指導要領や子供達の教科書等を参考に、作成者が個人的にまとめたものです。学習指導要領や各教科書および参考書等での、実際の括り方や 用いられている名称とは 異なる場合もありますので ご了承ください。
※ 調査や要約等には 細心の注意を払い、出来る限り正確な内容となるよう努めていますが、あくまでも全て、個人の解釈です。内容を保障するものではありませんので、ご了承ください。
おわりに
以上で、3年生算数【数と計算】領域の1回目について、各項目の詳細説明は終了です。
3年生のこの領域には10単元ありますので(※ 当ブログでの括り方です)、領域内の項目説明はまだまだ続きます!
次回は、「小学校算数3年生の項目詳細【数と計算】②」です。
それでは(^^)/